Chapter 3: Between Octaves
Other than Binary, there is another scaling ratio that is ubiquitous in nature.
Q: What ratio comes to mind that has a value between 1 and 2?
A: Phi - The Golden ratio
AKA THE fractal of the universe
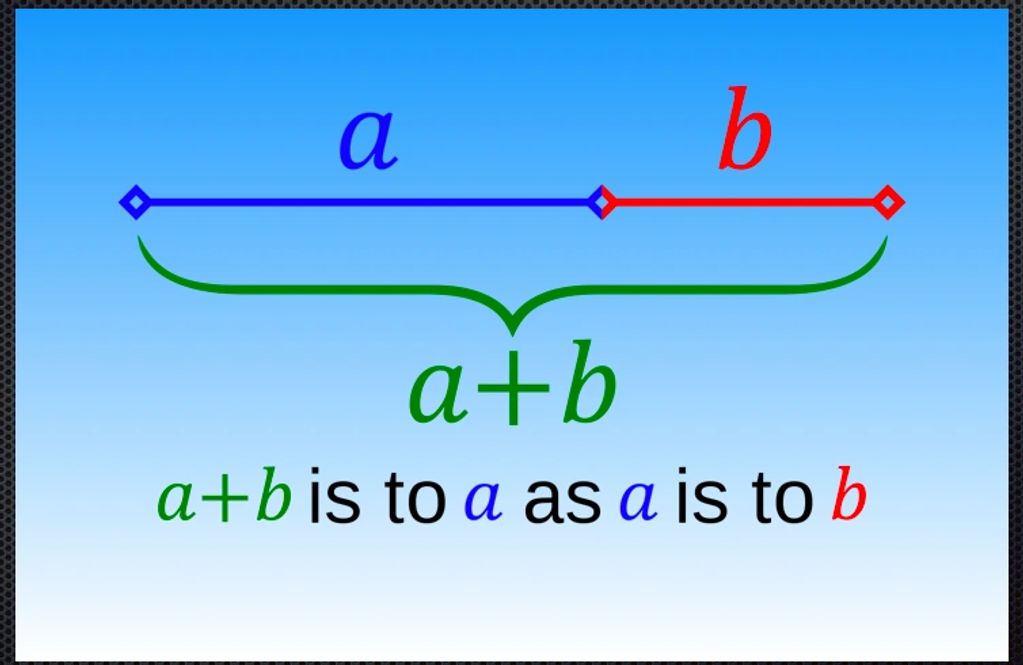
Divide a line segment into big and small such that: Whole is to big as big is to small. This is also known as Self similarity
Phi is also associated with 5-fold symmetry of a pentagon and can be written u
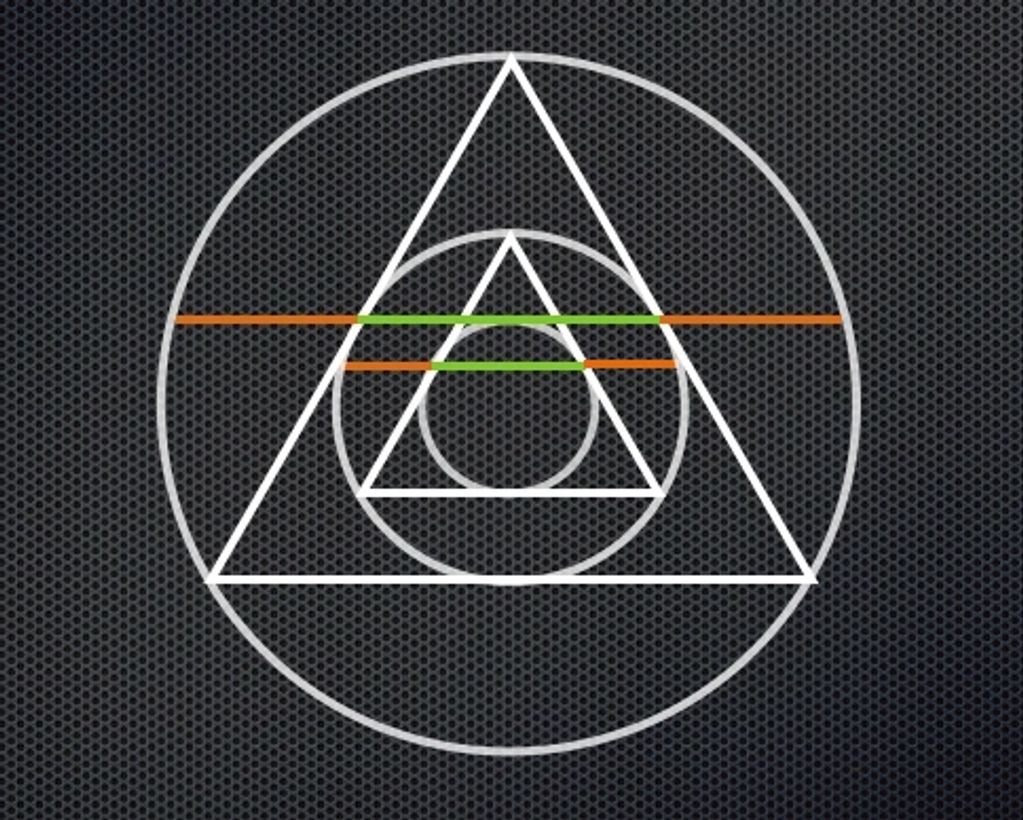
Where does Golden Ratio appear in our quantized grid?
Connecting the two octaves (inscribed and circumscribed circles of an equilateral triangle) through the midpoints of the sides creates phi proportions (seen here as ratio of green / orange segments)
"Binary is the container, Phi is the content!"
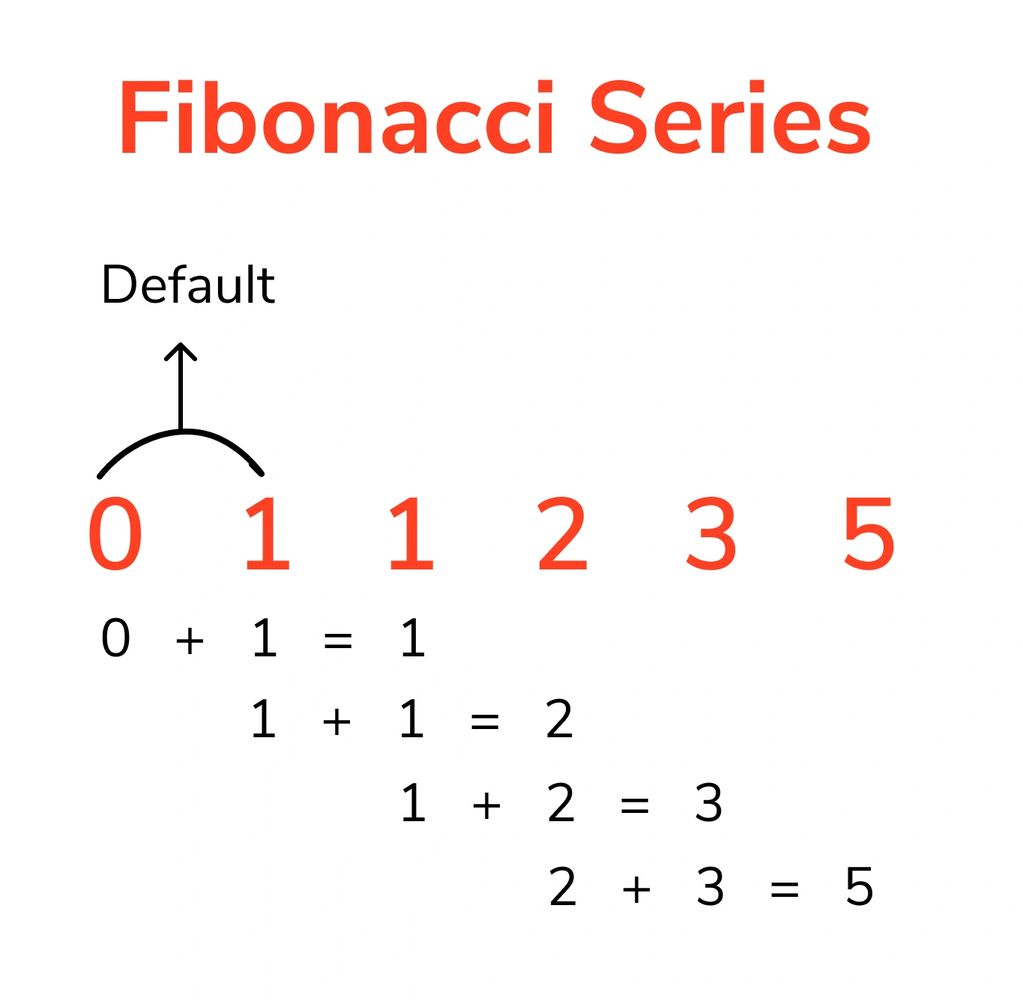
Almost synonymous with Phi is the Fibonacci series. It starts from 0,1 and each new number is generated by adding the previous two. This creates a recurring pattern of 'Trinity of numbers'.
This is also representative of the Feedback /Feedforward mechanism of a self organizing system, where the progression follows:
One step back / Two steps forward
This can also be related to the Alankar concept in
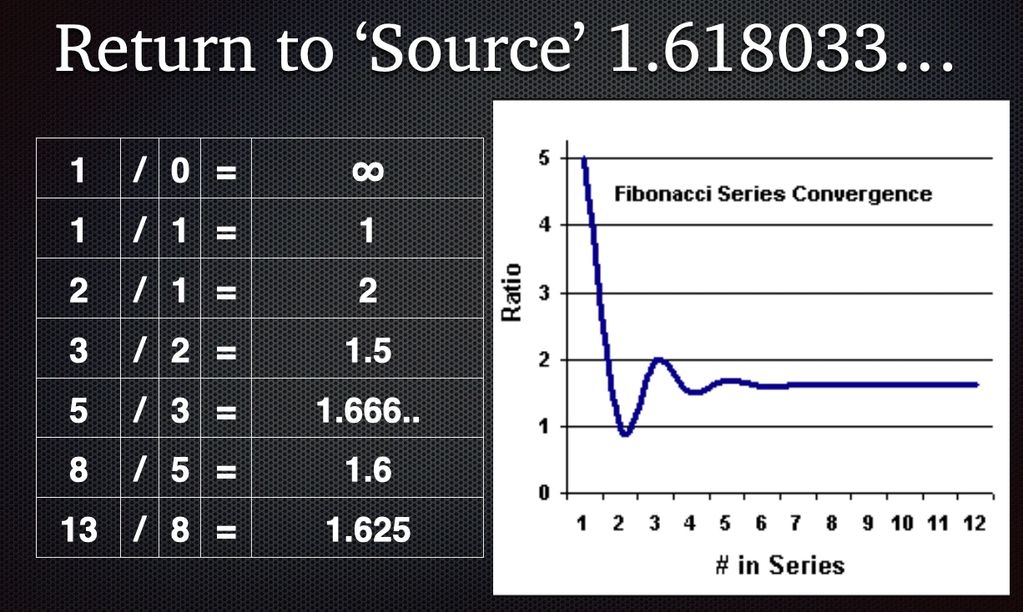
Fibonacci sequence starts as an arithmetic progression and ends up being a geometric progression (Φ^n).
In a way, we could call it a 'quantized' logarithmic scaling (in between +1 and x2)
According to Richard Merrick's 'Interference Theory', Fibonacci series is found in the Harmonic and Damping component of everything that emerges from and returns to equilibrium.
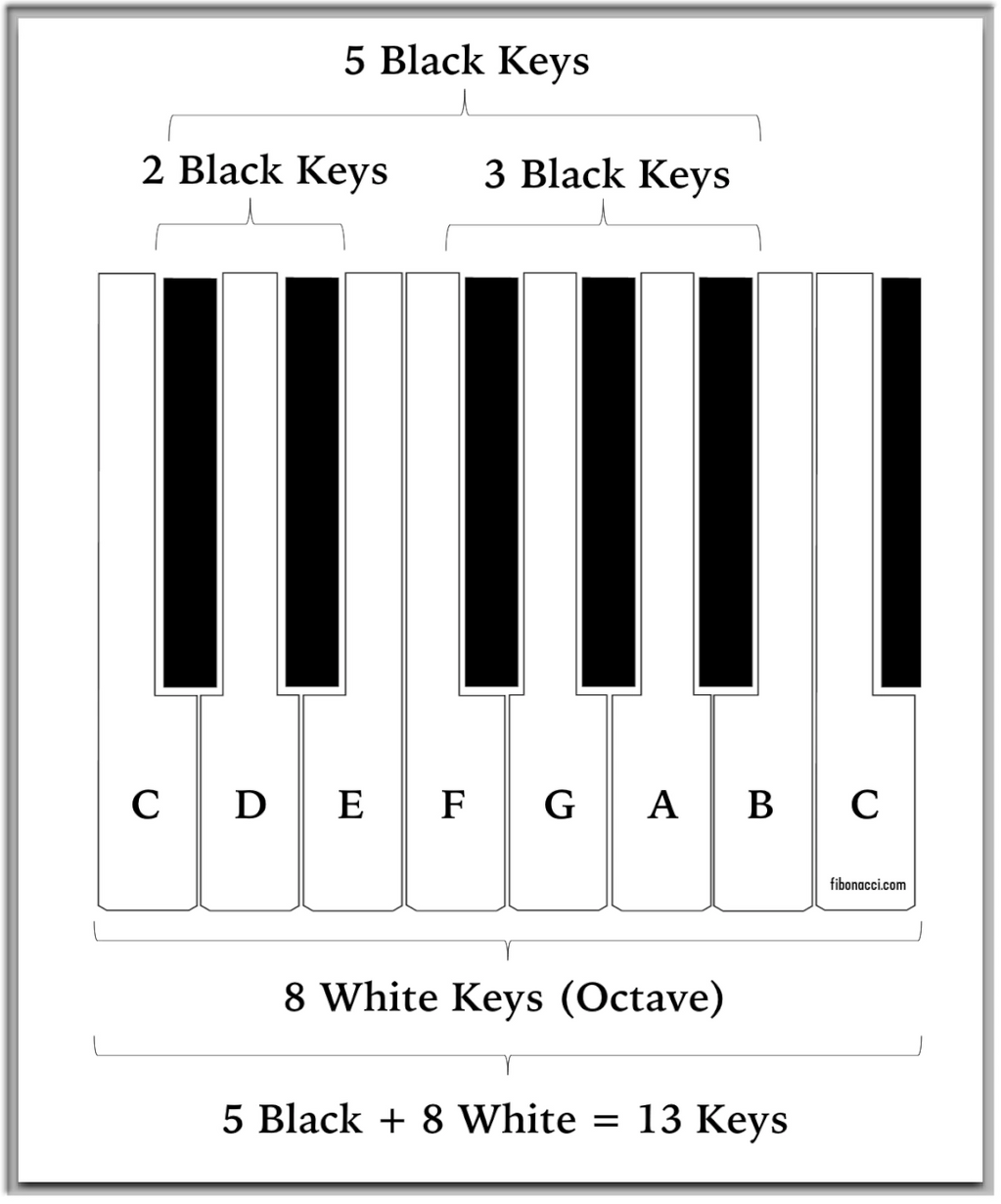
Where does Fibonacci appear between the octave?
The layout of a keyboard also displays this in a visually simple way.
According to Richard Merrick, the real magic lies in the acoustic interference pattern found between the root note and another sweeping tone (from root to octave) creating 12 gaps in the octave that can be described mathematically using fibonacci numbers.
More on interference theory:
The Cuboctahedron/VE (12 around 1) consists of alternating square and triangle faces. The triangle is the only stable shape in 2D and the square likes to jiggle.
This results in the cuboctahedron displaying a 'jitterbug' motion (see below) that produces 5 platonic solids.
In a sense, the cuboctahedron can be thought of as the 'mother' shape of all 5 platonic solids.
Balanced disequilibrium creates perfect shapes.
The fact that there can ONLY be 5 perfect shapes in 3D is one of the greatest Maths discovery of ALL TIME!
All Platonic Solids have Phi association either built-in or with relationship to the inner/outer spheres.
Also, the number of Vertices, Edges, and Faces have something in common. They are all ‘regular’ numbers i.e. numbers having only 2, 3, or 5 as
The 5 Platonic solids are made from only triangles, squares, and pentagons.
In fact, the next set of most symmetric shapes is the 13 Archimedean solids, which add the hexagon, octagon, and decagon to the mix. These three shapes are '2x duals' of 3, 4 and 5.
3,4,5 is also a Pythagorean triple!
3, 4 and 5 are made from 2, 3 and 5 because 4 is made from 2 x 2.
This is exactly what we need to generate A
Using the 5-limit tuning system, we can make up all the interval ratios using 'regular' numbers (multiples of 2,3 & 5).
This way, both the Platonic solids and the 5-limit scale have exactly the same "source code”.
NOTE: these intervals can also be interpretted as polyrhythms!
Another variation of this system is the 22 note system in India which is really an extension of the 12 note system.
The Indian system uses 5-limit JI system with 10 alternate derivations of all 12 notes except C&G, using higher powers of 2,3 and 5
- This system (of 22 'shrutis' as they are known) uses a syntonic comma of 81/80 = 22c to generate all the alternate derivations
- This is one such example of a 22 Shruti system
So a scale typically made of 7 notes is picked from a set of 22 notes.
22 and 7! Sound familiar?
Growth, Beauty and Efficiency are synonymous with Phi and Fibonacci!